The changing external conditions, we can get one of the three aggregate states. For the metal that does not experience allotropic transformations, that is, it exists with the single packing of atoms in the solid state, this dependence can be depicted graphically (Fig. 1).
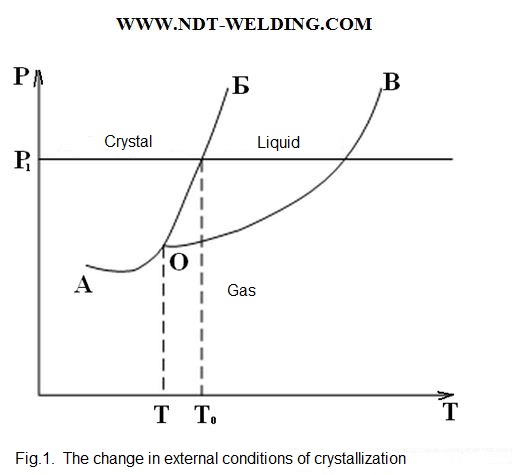
Ni, Cr, Cu – these metals do not experience polymorphic transformations.
At the constant pressure p1=const, at T0 in equilibrium there is the crystalline body and the liquid solution, that is, two phases are in equilibrium.
The phase is homogeneous part of the system, which has the same chemical and physical properties and has the partition surface.
The internal energy of the disordered liquid must be higher in the case of the ordered solid body, and in the transition from one state to another, the emission or absorption of heat should be observed.
The heat released during the transition of the liquid phase to the solid state is called the latent heat of the «L» fusion.
Let us establish the relationship between the crystallization temperature and the latent heat of fusion. At the crystallization temperature, the liquid and solid phases have the equal energies capable of producing external work, Gl = Gs.
Gl is the Gibbs free energy in the liquid, and Gs is the free energy of the solid phase. This quantity is called the thermodynamic potential, in contrast to the Helmholtz free energy.
-F=E – TS, Free energy can be determined:
G=E-TS+pV
where Е – Internal energy of the system, TS – related energy of the system, S – entropy, p– pressure, V – volume.
It is precisely because of the change in entropy in the transition of the liquid state to the solid state that it is possible to establish the relationship between the heat of melting and the crystallization temperature.
The enthalpy of the phase can be determined: H=E+pV
Free energy:
G=H-TS
At T0 :
HL-HS=T0SL-T0SS=T0ΔS
HL-T0SL=HS-T0SS
The difference in enthalpy (heat content) is the latent heat of fusion L=Hl-Hs.
We substitute in the above formula and obtain:
L=TEΔS or ΔS=L/Te
Thus, the measure of the change in the degree of order in the transition of the liquid phase to the solid phase can be obtained by dividing the latent heat of melting by the crystallization temperature.
When the crystals are formed with the packing of BCC, FCC, PG from the melt, the degree of entropy change is practically the same.
In the real conditions, at the equilibrium temperature, the crystallization process never begins. To start the crystallization process, always supercooling is necessary. It is visually represented on the crystallization curve of antimony (Fig. 2).
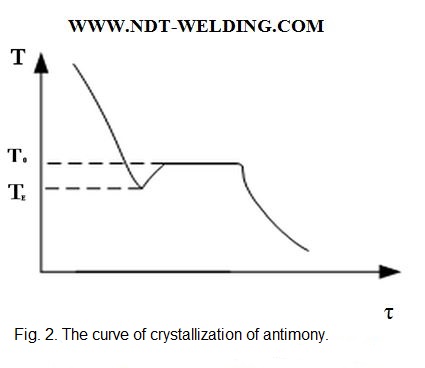
When the liquid is at the temperature below TЕ, it is said that the liquid is in a super cooled state. Once the crystallization has begun, the temperature of the remaining liquid rapidly rises to the normal crystallization temperature due to the release of latent heat of fusion.
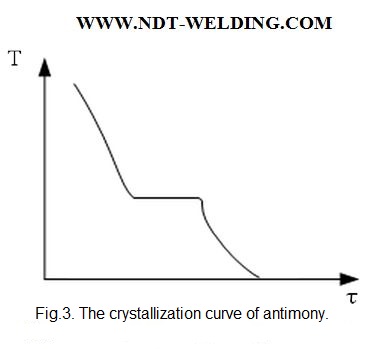
When crystallizing a small amount of metal, the heat released may not be enough to raise the temperature to equilibrium and then the crystallization will have the following form (Fig. 3)
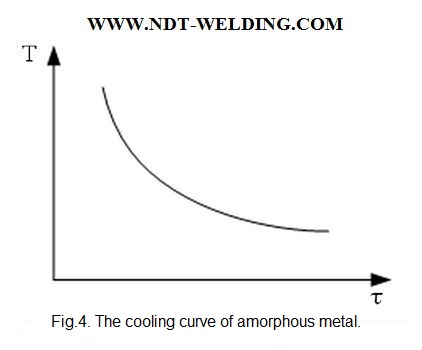
If the body during crystallization is amorphous, not associated with a change in the degree of order, latent heat is not released and the crystallization curve has the following form (Fig. 4)
The difference between the equilibrium temperature and the true crystallization start temperature is called the degree of supercooling.






